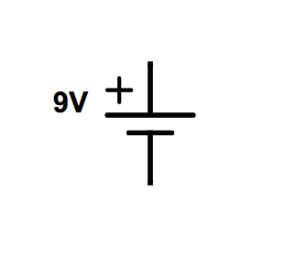Après avoir évoqué l'intensité et la tension du courant, voyons comment ces deux notions sont liées, en nous penchant sur l’équation la plus importante pour maîtriser les paramètres basiques d’un circuit électrique : la fameuse loi d’Ohm.


Nommée d’après son papa, le physicien Georg Simon Ohm, la loi d’Ohm marque l’origine, au XIXe siècle, de la théorie des circuits électriques.
Pour nos lecteurs et lectrices qui n’aiment pas beaucoup les mathématiques : n’ayez crainte ! La loi d’Ohm a un bon rapport complexité/utilité : elle est extrêmement simple, et incroyablement pratique.
Une loi pour les lier tous
On a donc exploré deux caractéristiques mesurables du courant électrique : intensité (I) et tension (U). Elles sont liées entre elles par l’équation suivante :
U = I x R
sachant que U est la tension, I l’intensité et R la résistance.
De façon générale, le terme résistance désigne la propriété qu’a n’importe quel conducteur de s’opposer au courant (au mouvement des électrons).
Ce nom vous rappelle sûrement un composant que nous avons survolé. C’est normal, car le composant « résistance » est fait spécifiquement pour présenter une résistance au courant. Toutefois, parce qu’il n’existe pas de conducteur parfait (avec une résistance nulle) tous les composants (diode, transistor, tubes, interrupteur, même les câbles) ont une certaine résistance interne. Assez souvent cette résistance est très faible (voire extrêmement faible, dans un câble, par exemple) mais certains composants ont une résistance interne non négligeable (c’est le cas des tubes).
Le couteau suisse
Pourquoi est-ce que la loi d’Ohm est si cruciale ? Parce qu’elle met en lumière la proportionnalité constante qui unit ces trois éléments : dans l‘équation ci-dessus, toute variation d’une des valeurs entrainera nécessairement la variation d’au moins une autre, si la troisième reste fixe (exemple : si pour la même résistance R, vous augmentez la tension U, alors l’intensité I augmentera aussi).
La loi d’Ohm a un autre avantage important. On peut transformer l’équation :
U = I x R
en I = U / R
et en R = U / I
Ainsi, à partir de ces trois formules, et dans tous les montages que l’on peut étudier ou créer, il suffit d’avoir deux éléments pour calculer le troisième. La loi d’Ohm permet donc, lorsqu’on ne peut pas la mesurer directement, de calculer la tension, l’intensité ou la résistance.
Quelques exemples
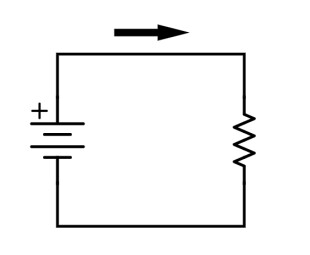
Prenons une source de courant continu de 9V, une pile par exemple. Voici son symbole schématique :
Les deux traits qui sortent, en bas et en haut, de ce symbole sont, si l’on veut, les deux bornes de la pile. Le côté positif est indiqué par un +. Rien de compliqué pour l’instant… Mettons cette pile en circuit :
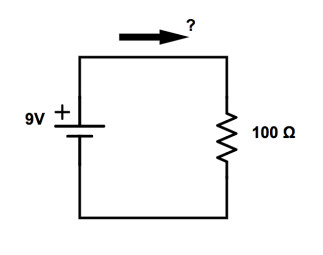
On a relié les deux bornes entre elles par une résistance de 100 Ω. Quelle est l’intensité du courant qui la traverse ? Puisqu’on connaît la valeur de la tension et de la résistance, on peut utiliser l’équation :
I = U / R = 9 / 100 = 0,09 ampères (A). On notera plutôt 90 milliampères (mA)
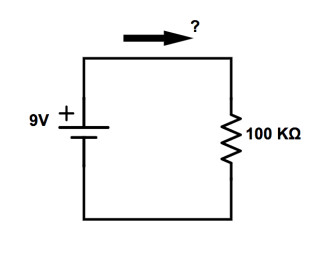
Puisqu’une résistance s’oppose au courant qui la traverse, il n’est pas surprenant que, si l’on augmente sa valeur, on obtienne un courant plus faible. Avec une résistance de 100 000 Ω (on la note plutôt 100 kΩ) :
On reste sur la même équation :
I = U / R = 9 / 100 000 = 0,00009 A, qu’on notera 0,09 mA.
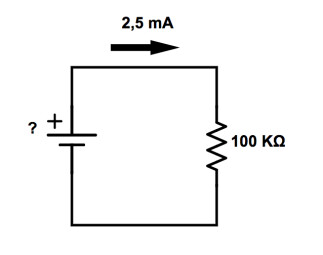
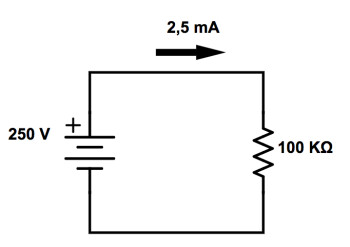
Dernier exemple, la résistance reste à 100kΩ, le courant augmente à 2,5mA (0,0025 A) et cette fois-ci c’est la tension d’alimentation qui est inconnue. Quelle tension a été fournie à ce circuit ?
U = I x R = 0,0025 × 100 000 = 250V (ce n’est plus une pile à ce niveau là !)
Et la puissance dans tout ça ?
En musique la notion de puissance est bien connue. Elle ne désigne pas seulement votre capacité à soulever un Twin Reverb mais l’analogie fonctionne bien : si vous voulez soulever une charge lourde, il va falloir fournir de l’énergie ; plus vous êtes puissant, plus vous fournirez cette énergie facilement et rapidement.
La puissance correspond donc au travail (la quantité d’énergie) fourni durant un temps donné. La puissance électrique se note P et se mesure en watts (W) et en électronique, elle aussi est liée à l’intensité et à la tension par une équation :
P = U x I
Elle est donc le produit de la tension et de l’intensité. Pourquoi ? Pour comprendre cette relation, voici un exemple simple : nous avons un générateur de tension et une résistance, montés en circuit.
Lorsque le courant traverse la résistance, le frottement des électrons en mouvement produit de la chaleur. Si elle est traversée par un courant suffisant, une résistance peut même devenir très chaude au toucher (elle peut même finir par cramer). Cette chaleur dissipée est l’expression de l’énergie.
Mais, un résistance est un composant passif, elle ne fait que résister : elle ne peut pas fournir d’énergie. Alors, nous devons en conclure que cette énergie provient d’ailleurs : du générateur. C’est logique, c’est lui qui fournit le travail pour faire se déplacer les électrons dans le circuit.
Rappelez-vous de la loi d’Ohm expliquée ci-dessus : si on augmente la tension, le courant traversant la résistance augmentera aussi. Alors, l’énergie fournie pour générer ce courant, et l’énergie dissipée par la résistance augmentera à son tour : voilà pourquoi les trois sont liés !
Lorsqu’on achète une résistance dans le commerce, il faut donc préciser sa puissance admissible, sinon attention les flammes… La plupart du temps ¼ de watt (0,25W), ou ½ watt (0,5W) sont tout à fait suffisants. Toutefois, il existe des résistances, plus grosses, faites pour dissiper des puissances bien plus élevées (dans nos amplis, on arrive parfois à des résistances de 5 ou 10 watts).
Reprenons le dernier exemple que j’avais utilisé. Il est intéressant car il utilise une haute tension : un circuit avec un générateur de 250V et une résistance de 100kΩ traversée par un courant de 0,0025A. La puissance dissipée sera de :
P = U x I = 250 × 0,0025 = 0,625 watts
Donc il nous faudra au moins une résistance de 1W admissible, si l’on ne veut pas trop risquer la surchauffe.