DEBAT : est-ce qu'on a moins de profondeur/niveau avec un mix seulement software/ordi?
- 1 172 réponses
- 79 participants
- 95 628 vues
- 129 followers
maxxsoultronik
une petite question.
Je viens de me mettre au mixage d'album rock. J'avais une assez longue expérience dans la production de musique électronique et j'ai eu envie de me diversifier.
Mes premiers mixs sonnent bien, les labels et artistes sont content. Cependant, perfectionniste dans l'âme, j'ai un petit soucis. Bien qu'il ne soit pas encore masterisé, j'ai l'impression que mes mixent manquent de profondeur, d'un peu de niveau, de présence... C'est difficile à expliquer. J'arrive progressivement à améliorer ce problème en renforçant l'image stéréo, la compression, en triggant la batterie, etc. Mais même après des heures passées à bosser de très bonnes prises réalisées dans un studio pros, j'ai toujours ce petit problème de rondeur-puissance-profondeur qui me manque un peu...
Alors ma question est :
- est-il possible d'avoir un mixage excellent, puissant et prifond, juste avec des plugs ins (sans hardware, ni table de mixage)?
- est-ce que le mastering amène réellement de la profondeur au mixage?
- est-ce que ce manque de grain, de pêche est le revert de la médaille d'utiliser uniquement un ordinateur?
Me conseillerez vous de repasser à la fin toutes mes pistes mixées dans une ssl ou une neve et de corrigier le tout pour gagner un peu en grain et en pêche?
MERCI ;)
scare
T'as fait un Edit ? ![]()
Construction du nouveau studio
Visitez le site THD STUDIO / page FB THD Studio
Dossier : Conversion analogique-numérique (pour les courageux)
J-Luc
![]()
![]()
Il y a deux moyens d’oublier les tracas de la vie : la musique et les chats.
Albert Schweitzer
Playskool17
Scare et J-Luc: par décision unanime, vous êtes virés tous les deux ! Non mais ! ![]()
J-Luc
Tu peux pas me virer, je suis modo. Modo vicinal, certes mais JE peux te virer, moi. ![]()
Hors sujet :
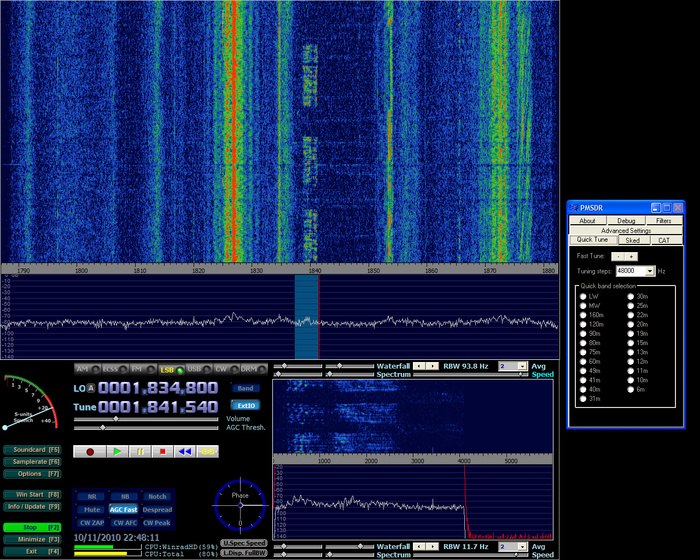
Pour changer de sujet en restant dans le sujet : Imaginez : on mélange une onde radio avec une sous-porteuse non pas décalée de 455 ou 1070kHz mais de... 0, du coup les produits du mélange sont dans le domaine audio. Le mélange se fait avec des portes analogiques qui sortent deux signaux I et Q en quadrature et on entre ça dans les bons convertisseurs audio d'une UA-1000 réglée sur 96kHz/16 bits.
Tout ça (sauf l'UA-1000) entre dans une boîte grosse comme rien connectée en USB au PC, à une antenne ondes courtes et à l'Edirol par un câble stéréo. On met un logiciel de SDR (Software Defined Radio) sur le PC et on obtient ... un récepteur ondes courtes qui m'a permis à l'instant de choper un collègue radioamateur français à Guernesey sur 1.8MHz (160mètres).
L'idée est de remplacer plein de matos HF par plein de logiciels. C'est pas encore terrible mais ça commence à être franchement rigolo. Pour info c'est l'interface son qui donne tout le gain et elle doit sampler exactement en même temps I et Q faute de quoi le décodage des divers modes de modulation échoue.
Vous savez quoi ? La carte son intégrée est très mauvaise et l'Edirol UA-1000 en USB-2 est comme le 5ème élément : par-faite.
Son ici et image ci-dessous.
Il y a deux moyens d’oublier les tracas de la vie : la musique et les chats.
Albert Schweitzer
[ Dernière édition du message le 10/11/2010 à 23:17:39 ]
Playskool17
Bon ben, là, ça y est, je suis largué ![]()
Zerosquare
Scare : la décorrélation entre le signal et le bruit de quantification, c'est l'une des hypothèses nécessaires pour que le suréchantillonnage en entrée fonctionne. Mais je suis d'accord que c'est faux lorsque l'amplitude du signal est très faible ; d'ailleurs, il me semble que certains convertisseurs rajoutent intentionnellement un peu de bruit blanc aléatoire pour "casser" la corrélation.
scare
Zerosquare : oui en rajoutant un dither
Construction du nouveau studio
Visitez le site THD STUDIO / page FB THD Studio
Dossier : Conversion analogique-numérique (pour les courageux)
Dr Pouet
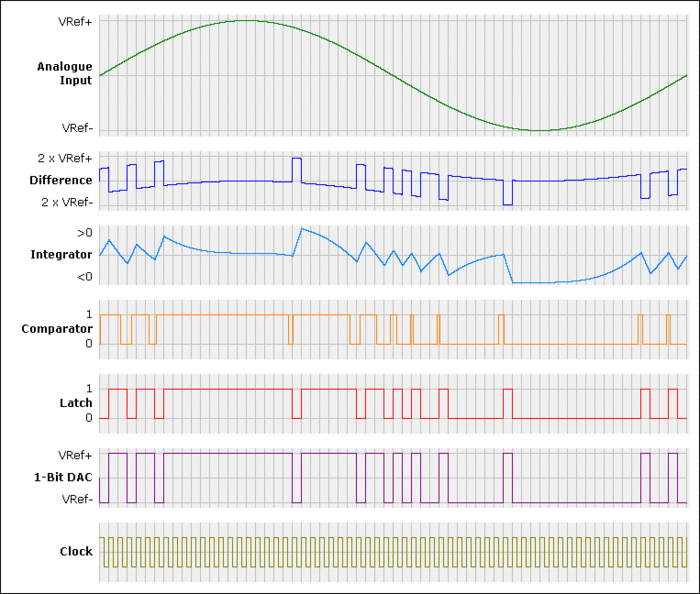
Les chronogrammes aident bien à comprendre.
Donc en fait les 0 et 1 du signal :
- n'indiquent pas s'il faut ajouter 1 ou retrancher 1 à la valeur courante de l'échantillon (ce qui poserait le problème de pente dont on parlait)
- ils indiquent en fait s'il faut ajouter 1 ou retrancher 1 à la pente courante du signal (c'est l'expression "delta est doublé " "delta est quadruplé" page 4 du doc mentionné par J-Luc)
Pour ceux qui ont déjà joué au joystick avec un simulateur de vol:
- imaginons que le 0 veuille dire "je tire à fond le manche"
- que le 1 veuille dire "je pousse à fond"
- que la vitesse sol soit constante
Si on veut faire un vol plat et vu qu'on a droit qu'au 0 ou 1, il faut successivement pousser puis tirer à fond. Ça fout mal au cœur, mais ça marche. Avec une série de 0, non seulement ça monte, mais ça monte de plus en plus vite.
Si on veut monter lentement, on fait : 00101010101010101
(deux fois 0 pour se mettre en montée, puis un vol plat)
si on veut monter rapidement : 0000000101010101010
Sur la figure 5 du lien ci-dessus : le latch est la commande de joystick, et le "analogue input" est la trajectoire de l'avion.
[ Dernière édition du message le 11/11/2010 à 00:46:02 ]
Dr Pouet
Convertisseur analogique / numérique :
http://www.beis.de/Elektronik/ADDA24QS/AD24QS.html
Tous les kits :
http://www.beis.de/Elektronik/Electronics.html
scare
Merci très intéressant ton doc.
Construction du nouveau studio
Visitez le site THD STUDIO / page FB THD Studio
Dossier : Conversion analogique-numérique (pour les courageux)
scare
OurDarkness wrote:Hello all,
I am new to this forum.
I want to buy a high end converter (I am between 3 brands) and I was wondering whether it is safe to assume that a converter running at 192 KHz can handle the 96 KHz sampling rate better than the 96 KHz unit? Dan said that the bigger the sampling rate the more chances of error there are, so I would like to know what these chances are and whether they are related to the clock per se or to the AD converter. Or, in other words if I get a 192 KHz unit and run it at 96 Khz are the chances of error less than if I had the 96 Khz unit and run it at 96 KHz?
Same question is for lower sampling rates: Dan's Gold AD is 96 KHz, does that mean that it's more accurate at 48 KHz?
Regards,
Yannis
An AD converter that can convert at 192KHz, can be made to operate at 1/2 the rate (96KHz) by a process called "decimation by a factor of 2". In fact most converters these days, the converter front end (the modulator) operates at very high rates, such as 64, 128, 256, 512 or even 1024 times faster then the sample rate. Bringing it down to a final rate (the sample rate) of 48KHz, or 96Khz or 192KHz is done by that decimation process.
But a 100MHz front end modulator can not yield good audio results. You can keep decimating down, but even a theoretically perfect decimation will not save you from high distortions and noise. The limitations are already there in the modulator.
The designer faces a tradeoff regarding the basic converter architecture. The question is: shell I optimize the design for 96 KHz? Or for 192 KHz? This is a conceptual and theoretical decision, before you even begin the hardware design.
Take a sigma delta architecture (as in most converters today), and you have some basic parameters to play with: Modulator front end speed, modulator order (how many bits in the front end), filter order (the feedback loop). So for any given set of such parameters (fixed resources), one can trade off the final desired bandwidth against accuracy (distortions and noise). In other words, “holding all things equal”, one can trade off speed against accuracy. This is a “block diagram” tradeoff right from the get go.
Say you want to dig a hole for a swimming pool. You have the resources to dig 100 cubic feet. One can dig a 1 square foot area to 100 feet of depth. Or on can dig a 100 square feet area but only 1 foot deep. Or one can dig a 20 foot area at 5 feet depth… That is an analogy for the modulator design. One needs to plan for an optimized outcome, before you even started digging. You want enough area to swim, but it also needs to be deep enough. In the case of audio, one wants to have enough bandwidth, which is dictated by how much the ear can hear, but the more bandwidth is not free – it reduces accuracy. It is a tradeoff! If you believe that your ear can hear 96KHz then you may opt for 192KHz. If you think that the ear can hear up to 48KHz, then 96KHz may be of value. The fact is – 96KHz sampling is already too high.
Not less important is the real hardware design. A circuit that operates faster, will yield larger error. Say you need to charge a capacitor, if you have more time, you can reach better precision. If you apply a step into an opamp, it will settle to a more accurate value when you take more time. And so on… Note that charging caps and settling opamp IS at the hart of convertors…
I talked about AD’s but DA’s are similar. They too have a modulator, and the tradeoff is also there right from the start, as well as the limitations due to circuit limitations due to speed – accuracy tradeoff (charging caps, settling opamps and much more).
A 192KHz AD and DA are device that can capture or reproduce signals that occupy up to 96KHz signals. But you simply do not need that for audio. That is a ridicules bandwidth in a world of mics and speakers (mostly 20KHz devices). It is a bad tradeoff.
A converter that allows you to process signals you do not need such as over 50KHz has a BUILT IN traded off, and one can not fixed the accuracy issues after the fact, by decimation from 192KHz to 96KHz. The accuracy is already reduced before the decimation.
A converter that does a good job at 192KHz will likely do as good job at 96KHz (not better). But given the same “fixed resources” a designer can get better results when aiming at 96KHz. Of course a converter optimized for 96KHz can not accommodate signals above 48KHz. Is that a good trade-off? My dog does not hear 48KHz…
Regards
Dan Lavry
Construction du nouveau studio
Visitez le site THD STUDIO / page FB THD Studio
Dossier : Conversion analogique-numérique (pour les courageux)
scare
Construction du nouveau studio
Visitez le site THD STUDIO / page FB THD Studio
Dossier : Conversion analogique-numérique (pour les courageux)
scare
Hello Dan,
Je viens de lire votre pdf sur la théorie de l'échantillonnage ... Vous dites 192 kHz est trop élevé pour obtenir une bonne qualité audio, mais est ce que 96 Khz l'est aussi ?
Tout cela devient confus.
Réponse ici
![]()
Construction du nouveau studio
Visitez le site THD STUDIO / page FB THD Studio
Dossier : Conversion analogique-numérique (pour les courageux)
Pere Founasse

Provocateur d'extrême droite
[ Dernière édition du message le 11/11/2010 à 04:06:14 ]
DiZ69
J'adore ce thread, un milliard de discutions croisées, de l'humour, du sérieux, de l'OVNIesque ^^
pour un thread qui devait finir en combat de troll, et sombrer dans l'oubli
quel volontarisme ! continuez les gars!
Danguit
Citation :L'idée est de remplacer plein de matos HF par plein de logiciels. C'est pas encore terrible mais ça commence à être franchement rigolo.
Dans le domaine professionnel, beaucoup de récepteurs nouvelle génération sont entièrement numériques. Pour les amateurs, cf. Ettus Research par exemple.
J-Luc
Danguit> je sais bien mais là tu verrais comme ça marche avec rien ! Bon, au delà de 10MHz, ça commence à plus aller; avec de fausses porteuses un peu partout. Ce qui est impressionnant dans le PMSDR que j'utilise c'est qu'il n'y a pas de front-end HF. pas un préamp HF, pas un MOS, rien ! Antenne -> mélangeur -> amplis op -> carte son.
Il y a deux moyens d’oublier les tracas de la vie : la musique et les chats.
Albert Schweitzer
J-Luc
Citation de Dr Pouet :
- ils indiquent en fait s'il faut ajouter 1 ou retrancher 1 à la pente courante du signal
VOILA ! C'est LA explication simple dont on avait besoin et l'analogie avec le joystick est parfaite. C'est ça l'intégration réussie ! ![]()
Il y a deux moyens d’oublier les tracas de la vie : la musique et les chats.
Albert Schweitzer
Zerosquare
Citation de : J-Luc
C'est ça l'intégration réussie !
![]()
Dr Pouet
Bon ça colle avec l'interrogation sur la pente ; mais la manière de se ramener à des mots de 16 ou 24 bits n'est pas encore claire pour moi.
44,1 Khz est-ce suffisant pour l'audio ?
Ils ont de la patience, pour tenter de convaincre que Nyquist ne s'est pas trompé... !
Je viens de lire votre pdf sur la théorie de l'échantillonnage ... Vous dites 192 kHz est trop élevé pour obtenir une bonne qualité audio, mais est ce que 96 Khz l'est aussi ?
Tout cela devient confus.
Dans celui-là (celui du 2ème message de scare) il donne clairement sa conclusion :
The good question to ask is what is the ideal sample rate. I believe the number is in the 60KHz-70KHz range for the optimum - fast enough to contain 30KHz in theory, and certainly more then 25KHz in practice.
Going faster only reduces accuracy, increases file size and demands more processing power for what we do not hear.
We do not have a 60KHz-70KHz standard, so 88.2KHz is a bit fast but not too bad.
Avec, un peu plus bas, un explication somme toute concrète et logique :
Quelle que soit l'année où on se trouve, un composant électronique fournira toujours une mesure plus précise à une fréquence basse qu'à une fréquence élevée. Au fil du temps, la qualité de la mesure à une fréquence donnée va s'améliorer, mais il restera quand même vrai que la même technologie sera plus précise à une fréquence plus basse.
Du coup il faut juste savoir de quelle fréquence on a besoin. D'après Lavry c'est Nyquist + un peu de marge, donc un idéal vers 60 70 kHz, donc soit 44kHz soit 88kHz puisque ces fréquence intermédiaires ne sont pas usitées.
[ Dernière édition du message le 11/11/2010 à 13:57:36 ]
scare
L'une des réponses de M. Lavry m'a tellement plu que je souhaite la faire partager à tout le monde dans notre bonne vieille langue.
J'ai essayé de la modifier un poilou en détaillant pour la rendre accessible même pour le newbie (j'ai dit "essayé" ![]() ). Logiquement ça intéresse toute personne pratiquant la MAO.
). Logiquement ça intéresse toute personne pratiquant la MAO.
La question : 44,1 Khz est-ce suffisant pour l'audio ?
Le théorème d'échantillonnage établi que l'on doit échantillonner deux fois plus rapidement que la période correspondant à la plus haute fréquence du spectre audio (FE = 2 fois la bande passante audio).
Lorsque le signal audio se situe à une fréquence proche (20kHz) de la fréquence de Nyquist (22,05 kHz), beaucoup de personnes ne regardent qu'une seule période du signal échantillonné. Ils se demandent alors comment il est possible de reconstituer la fréquence de 20 Khz avec seulement deux points issus de l'échantillonnage (un point toute les 22.67us pour une période de 50 us). C'est une vue erronée de l'échantillonnage. On ne peut pas dire que la forme d'onde est reconstituée seulement à partir de deux points, sur une seule période.
Pour comprendre l'échantillonnage, on doit prendre en compte plusieurs périodes de la même fréquence plutôt que seulement une période contenant seulement deux points d'échantillonnage.
En prenant plusieurs périodes, on se rend vite compte que les échantillons (points) atteignent des valeurs différentes sur chacune des périodes précédentes. Avec les données de multiples périodes, on peut alors reconstituer l'onde d'origine de l'échantillon tout en ayant seulement deux points par période.
Donc non seulement il faut respecter le théorème de Nyquist MAIS plus le signal audio s'approche de la fréquence de Nyquist (22,05 kHz pour une FE de 44,1 kHz), plus il faut de période du signal audio pour pouvoir reconstituer l'onde d'origine.
Cela me parait fondamental !! on l'on y pense jamais vraiment ! (en tout cas moi)
On notera que les périodes les plus récentes (plus proche de la portion audio en cours de reconstitution) contribuent davantage à la reconstruction. Il est juste de noter que ce qui s'est passé il y a plusieurs périodes a moins d'influence sur le résultat. Mais on ne peut ignorer les échantillons précédents, plus l 'historique du signal sera pris en compte, meilleure sera l'onde reconstruit. Bien sûr, il existe des limites pratiques à la façon dont nous regardons "en arrière".
À basses fréquences audio, il existe de nombreux échantillons dans chaque période du signal (car on se situe à une fréquence très basse par rapport à la fréquence de Nyquist).
Mais en augmentant la fréquence audio, nous arrivons à un point où il y a seulement 2 échantillons par période (au dessus de 8819 Hz), et le signal échantillonné devient visuellement déroutant pour ceux qui considèrent qu'une seule période (il ne ressemble plus du tout au signal original analogique). Un examen plus approfondi montre que les échantillons "marchent" au travers des cycles audio. En regardant le signal échantillonné sur plusieurs périodes, on observe que les échantillons sont décalés et l'on comprend comment reconstituer le signal d'origine.
En prenant une certaine période comme un «point de départ". De nombreuses période plus tard, nous avons attendu assez de temps pour retrouver un échantillon se trouvant assez étroitement à la même position que l'échantillon de la période du point de départ, la boucle est bouclée. on appelle cela «une période cyclique». cette période cyclique est répétitive (pour une onde sinusoïdale ou une entrée périodique).
Si nous voulions reconstruire par exemple 22049Hz avec une FE de 44,1 kHz (Nyquist à 22,05 kHz), le temps requis (pour atteindre même une approximation grossière) pour atteindre le point de départ de la "période cyclique" serait énorme. C'est parce que la différence de fréquence entre 22049 Hz et la fréq de Nyquist n'est que de 1HZ. Cette différence 1Hz a un donc une "période cyclique" de 1 seconde !!
Cela signifie qu'à une FE de 44,1 kHz, , pour obtenir suffisamment d'échantillon nécessaire à la reconstruction de la fréquence de 22049 Hz, il faut 1 seconde, soit 44100 échantillons ! C'est vraiment beaucoup de données à recueillir et filtrer ...
Cependant, disons que nous voulons reproduire proprement 20KHz avec le même Nyquist, alors la différence de fréquence est 2050Hz qui a une "période cyclique" de seulement 487 usec. Il ne faut alors que 21 échantillons de données pour atteindre une "période cyclique".
Combien de "période cyclique" a-t-on besoin pour que la reconstruction soit bonne? Cela doit être quantifié, mais il est clair qu'une reconstruction de 22049Hz avec 44,1 échantillonnage n'est pas possible ! D'autre part, une reconstruction de la qualité de la fréquence de 20KHz est possible.
Ainsi, au lieu d'essayer de faire une conversion très proche de la fréquence de Nyquist, nous descendons légèrement la fréquence de coupure du filtre afin de filtrer les signaux de telle sorte que le convertisseur n'ai pas besoin d'essayer de reconstruire ce qui est pratiquement impossible. Bien sûr, avec les nouveaux convertisseurs (Oversampling en entrée cf sigma delta), la fréquence de Nyquist est plus élevée par de facteurs énormes (dans la gamme MHz) et la question de l'anti aliasing sur les filtres des convertisseur AD appartient au passé (cela fut un problème jusqu'au début des années 1990). La même chose vaut pour la reconstruction DA qui est filtré après oversampling.
La question existe pour le "down sampling" (décimation), par exemple à 44,1 kHz avec les filtres numériques FIR ou IIR's. Pour obtenir le FIR plus proche de Nyquist, on doit filtrer plus longtemps, et pour décimer à 22.049 KHz, il nous faudrait sans doute des centaines de milliers d'échantillons et un énorme moteur de calcul. Ce n'est pas la peine. Si vous êtes prêt à se contenter descendre la bande passante 1000Hz en dessous de Nyquist, le problème devient beaucoup plus facile (Une "période cyclique" étant 1000 fois plus courte). il est alors possible de faire la décimation avec une quantité raisonnable de données. De la même façon faire l'IIR a ses limites aussi.
La question fondamentale est donc : Quelle est réellement la bande passante de l'audio ?!
Si l'on considère que c'est 20 kHz, alors aucun soucis pour travailler à 44,1 kHz.
Si l'on considère que c'est un peu plus, M. Lavry démontre que ça risque de partir assez vite en sucette en se rapprochant de Nyquist, alors mieux vaut travailler à 48 kHz pour décaler un peu plu., Mais dans ce cas nous n'obtenons pas une division entière lors de la redescente à 44,1 sur cd => 88,2 kHz semble peut être assez approprié.
Une Fe de 55,125 kHz serait vraiment au top, un bon compromis entre bande passante (275625 Hz), souplesse pour la reconstruction du signal d'origine, précision de l'électronique, quantité de données stockés.
Pour redescendre à 44,1 kHz, il faudrait simplement diviser la freq par 1,25, soit 1.01 en binaire
En étant un peu plus gourmand, une FE à 66,15 kHz. Pour redescendre à 44,1 kHz, il faudrait simplement diviser la freq par 1.5, soit 1.1 en binaire.
44,1 c'est peut être un poilou juste et 88,1 un poilou too much. Le mieux est d'abandonner le CD et de se mettre à 48kHz.
![]()
Construction du nouveau studio
Visitez le site THD STUDIO / page FB THD Studio
Dossier : Conversion analogique-numérique (pour les courageux)
[ Dernière édition du message le 11/11/2010 à 17:03:15 ]
Zerosquare
Danguit
Si j’en crois mes vieux cours, on commence par se fixer une fréquence max, par exemple 20kHz, ce qui donne une fréquence de Shannon à 40kHz, et on se fixe un coefficient de suréchantillonnage de # 1.1 (=> Fe # 2.2 Fmax) permettant de réduire la distorsion vers Fmax (je passe sur les détails).
Si tout cela est vrai, disserter sur ce qui se passe entre Fmax et Fe/2 présente peu d’intérêt. Mais je peux me tromper !
Dr Pouet
Je ne suis pas un spécialiste du traitement de signal et je n’ai peut-être pas tout compris, mais j’ai l’impression que le sieur Lavry présente le problème à l’envers.
Si j’en crois mes vieux cours, on commence par se fixer une fréquence max, par exemple 20kHz, ce qui donne une fréquence de Shannon à 40kHz, et on se fixe un coefficient de suréchantillonnage de # 1.1 (=> Fe # 2.2 Fmax) permettant de réduire la distorsion vers Fmax (je passe sur les détails).
Si tout cela est vrai, disserter sur ce qui se passe entre Fmax et Fe/2 présente peu d’intérêt. Mais je peux me tromper !
Ça va encore ressembler fortement à un argument d'autorité, et ce n'est pas le but, mais globalement on peut faire confiance à muster Lavry :
http://www.lavryengineering.com/innovationpage.html
Il a commencé à s'intéresser au problème des convertisseurs dans les années 70, a travaillé pour l'industrie des télécommunications (ITT, ATT), médicale, mesures (HP, Siemens), et conçu pour eux de nombreux produits.
A l'époque où Apogee ne fabriquait que des filtres, il s'est joint à eux pour se lancer dans les convertisseurs numériques, et a conçu les Apogee AD500 et DA1000. Bref, ce n'est pas le premier forumeur venu, il parle vraiment de ce qu'il connait. De plus, il est hyper cordial, jamais prétentieux, n'avance pour ainsi dire jamais l'argument d'autorité (à l'inverse d'autres "spécialistes" hautains évoqués plus tôt) et passe quand même un temps dingue à expliquer des trucs de base, comme le critère de Nyquist/Shannon.
Après, je suis comme toi : souvent je lis un truc qui me semble contradictoire avec ce que je sais déjà, donc j'aimerais bien une explication, même si c'est Lavry qui a écrit le texte !
Et même si ça doit lui arriver de se tromper, et surtout de s'emmêler dans une explication, ça doit quand même être assez rare !
lm
Citation de : scare
L'une des réponses de M. Lavry m'a tellement plu que je souhaite la faire partager à tout le monde dans notre bonne vieille langue.
Merci Scare, d'avoir traduit cette réponse de Dan Lavry et du coup de rendre compréhensible (au moins en partie) pour les néophytes dans mon style le débat fourni que vous avez entre spécialistes.
- < Liste des sujets
- Charte