Les montages en parallèle - Bien débuter en électronique : partie 10

Je ne doute pas que certains lecteurs-musi­ciens ont déjà entendu ces termes (ou les ont employés), en parti­cu­lier dans le cadre de la connexion des hauts parleurs à la sortie d’un ampli­fi­ca­teur. Mais proba­ble­ment sans toujours comprendre ce dont il retourne. Entrons direc­te­ment dans le sujet…

Paral­lèle / série : les bases

Deux compo­sants sont montés en paral­lèles lorsque leurs bornes respec­tives sont direc­te­ment connec­tées entre elles.

Prenons deux résis­tances : on voit bien comment leurs bornes sont chacune connec­tée avec l’autre.

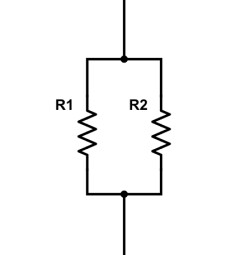
Le même type de montage existe donc poten­tiel­le­ment pour tous les compo­sants dipôles (conden­sa­teur, auto-induc­tion, diode…). De plus, il n’est pas néces­saire de se limi­ter à deux compo­sants : 

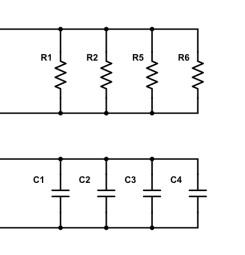
Exemple avec quatre résis­tances ou quatre conden­sa­teurs

Ni au même type de compo­sant : 

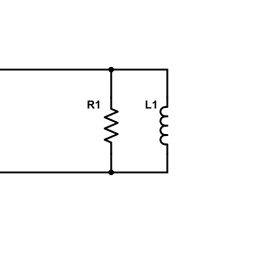
Une résis­tance et une induc­tance en paral­lèle

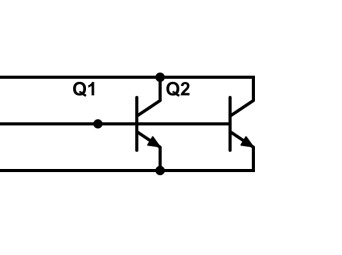
Pour finir, peut-on monter en paral­lèle un compo­sant qui a plus de deux bornes, comme un tran­sis­tor ? Voici deux tran­sis­tors NPN montés en paral­lèle. La ligne centrale qui « traverse » Q1 repré­sente la connexion qui relie entre elles les bases des deux tran­sis­tors.

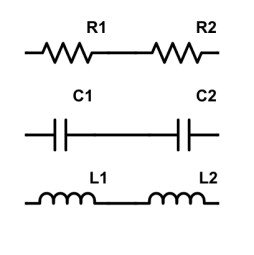
En série, les compo­sants se suivent. Là aussi, on peut faire s’en­chaî­ner des compo­sants de même type, ou diffé­rents.

On comprend donc que ces deux types de montage forment l’in­té­gra­lité des possi­bi­li­tés d’as­sem­blage de compo­sants entre eux. Toute partie d’un circuit peut se comprendre comme des ensembles de compo­sants en paral­lèle et/ou en série. Nous revien­drons sur cette notion, mais avant, posons quelques règles.

Calcul des résis­tances en paral­lèles

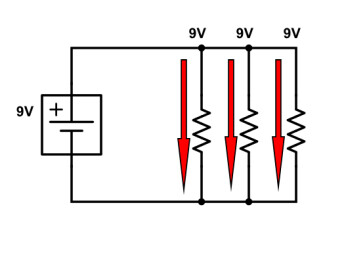
Si l’on applique une tension aux bornes d’un réseau de résis­tances paral­lèles

La tension sera égale aux bornes de chaque résis­tance. Pour ce qui est du courant, chacune résis­tera à son passage, plus ou moins, selon sa valeur. Ainsi, chaque résis­tance sera traver­sée par un courant propor­tion­nel à la tension à ses bornes (ici 9V) et à sa valeur résis­tive. Je le sais grâce à la Loi d’Ohm. Faisons-en la démons­tra­tion : si les trois résis­tances ont pour valeur 100Ω…

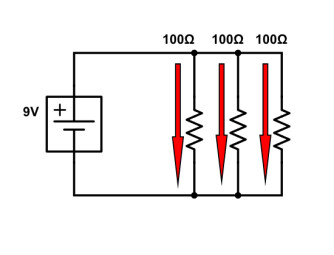
On connaît la tension, et la valeur de chaque résis­tance. On peut en tirer une équa­tion à une incon­nue, à partir de la loi d’Ohm. Ainsi, on pourra calcu­ler l’inten­sité du courant qui la traverse de la façon suivante :

I = U/R = 9/100 = 0,09 ampère

Comme nous avons trois résis­tances de même valeur, chacune sera traver­sée par un courant d’une inten­sité de 0,09 ampère. La somme du courant total dans le circuit sera donc de 0,09 × 3 = 0,27 ampère (270 mA).

Si l’on mesure l’in­ten­sité avant ou après le réseau de résis­tance, on obtien­dra le même résul­tat, car le courant se répar­tit dans chaque résis­tance puis se recom­bine à leur sortie : cela se nomme la Loi des Nœuds.

Ques­tion piège : on sait que le courant rencontre trois résis­tances, chacune de 100Ω, mais quelle est la valeur totale de la résis­tance rencon­trée par le courant ? S’agit-il d’une simple addi­tion, 100+100+100 = 300 Ω ? Eh bien non, et nous avons deux moyens de le comprendre.

Premiè­re­ment, nous pouvons à nouveau utili­ser la Loi d’Ohm. Nous connais­sons l’in­ten­sité du courant total (0,27 A), et la tension (9 V) : trai­tons la résis­tance comme une incon­nue. Cela donne : 

R = U/I = 9/0,27 = 33,33 Ω

La résis­tance total (Rt) est donc moindre que chaque résis­tance indi­vi­duelle !

Pourquoi ? Deuxième manière de comprendre : l’ana­lo­gie avec les flux liquides. Imagi­nez un tuyau bran­ché à la sortie d’un robi­net. L’eau, c’est notre courant ; le tuyau, c’est la résis­tance. Le diamètre fin du tuyau limite la quan­tité d’eau qui peut couler à travers lui (comme une résis­tance). Vous ouvrez le robi­net pour donner une certaine pres­sion d’eau (la tension) : le tuyau laisse passer toute la quan­tité d’eau que son diamètre permet. Mais si vous instal­lez une bifur­ca­tion, un deuxième tuyau qui part en paral­lèle au premier, vous augmen­tez la capa­cité du système de tuyaux à trans­por­ter de l’eau. Vous n’avez pas touché le robi­net, donc la pres­sion (la tension) reste la même, seule la capa­cité de lais­ser passer l’eau a augmenté ! Plus de tuyaux signi­fie donc moins de résis­tance au passage de l’eau.

Plus de résis­tances montées en paral­lèle signi­fie donc… Une moins grande résis­tance au courant.

Et si les résis­tances n’ont pas toutes la même valeur ? Dans ce cas-là, le courant se répar­tit propor­tion­nel­le­ment à la valeur de chaque résis­tance, un peu dans l’une, plus dans l’autre, selon la capa­cité de chacune à résis­ter à son passage. Mais le résul­tat est le même : la valeur totale sera infé­rieure à la valeur de la plus petite des résis­tances.

Pour être complet, voici l’équa­tion qui permet de calcu­ler la valeur totale : 

1/R = 1/R1 + 1/R2 + 1/R3…

Si les résis­tances montées en paral­lèle ont toutes la même valeur (comme dans notre exemple ci-dessus, avec 3 résis­tances de 100 Ω), on peut simpli­fier cette équa­tion : il suffit de divi­ser la valeur d’une des résis­tances par leur nombre (ci-dessus : 100 Ω / 3 = 33,33 Ω).

NB : pour les moins matheux, il existe aussi des calcu­la­teurs en ligne qui fonc­tionnent très bien…

Dans la réalité du circuit

Avant d’al­ler plus loin, je souhaite préci­ser les réali­tés de montage en paral­lèle dans les cicuits.

Les exemples ci-dessus conviennent pour expliquer des montages extrê­me­ment simples, mais que l’on rencontre assez rare­ment en tant que tel. En effet, au sein d’un circuit élec­tro­nique complexe, une majo­rité des compo­sants sont de facto montés en paral­lèle les uns par rapport aux autres. Prenons l’exemple d’un étage d’am­pli­fi­ca­tion à tran­sis­tor, montage émet­teur commun : ici V1 repré­sente sché­ma­tique­ment une source de tension alter­na­tive, c’est-à-dire poten­tiel­le­ment une source audio…

Dans ce schéma, quels compo­sants sont montés en paral­lèles ? On distingue deux groupes. D’abord, en paral­lèle la source de tension, avec les résis­tances R2, R4 et le conden­sa­teur C2.

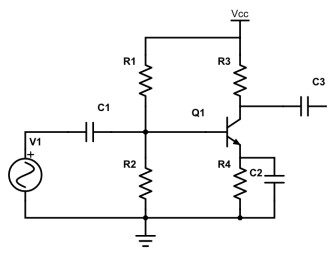
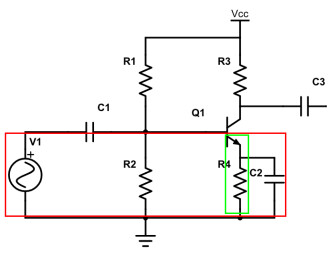
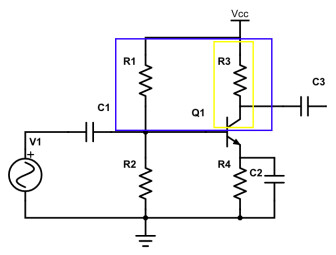
Si l’on veut être très précis, il faut signa­ler qu’au sein des compo­sants en paral­lèle R4 forme un couple avec la jonc­tion base-émet­teur du tran­sis­tor (ici enca­dré en vert). En effet, souve­nez-vous, nous avions parlé des jonc­tions PN dans les tran­sis­tors : dans un tran­sis­tor NPN, comme celui de notre exemple ci-dessus, il existe une jonc­tion PN entre la base et l’émet­teur et un autre entre la base et le collec­teur. Il faut donc les prendre en compte dans la somme des compo­sants montés en paral­lèle. Égale­ment dire que C2 est plutôt en paral­lèle avec R4.

Deuxième groupe, ci-dessus : R1 et R3 + jonc­tion base-collec­teur (en jaune).

Conden­sa­teurs en paral­lèles

Beau­coup plus simple ! Là aussi la tension aux bornes de chaque conden­sa­teur reste égale, elle est seule­ment dépen­dante du géné­ra­teur à l’en­trée du circuit.

Ce qui nous inté­resse, c’est la capa­cité © de charge totale : comme on l’avait vu un conden­sa­teur possède une capa­cité à stocker du courant et à le resti­tuer (comme une pile rechar­geable, si l’on veut). Cette capa­cité se note le plus souvent en micro-farad (le farad étant très gros). Si l’on met plus d’un conden­sa­teur dans un circuit, que se passe-t-il du point de vue de la capa­cité ? Elle augmente par addi­tion, tout simple­ment. On trouve donc : 

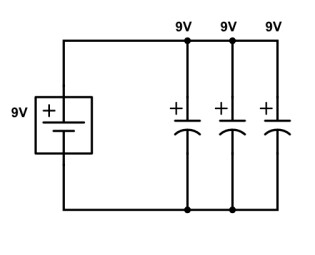
C = C1 + C2 + C3…

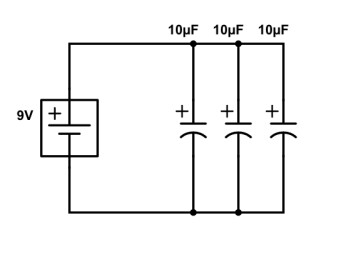
Par exemple ici : 

Cela donnera C = 10 + 10 + 10 = 30 µF

Pour ce qui concerne l’inten­sité dans un circuit avec des conden­sa­teurs en paral­lèle, sachez que plus la capa­cité d’un conden­sa­teur est élevée, plus il peut se char­ger, et plus il peut ensuite déli­vrer du courant. On comprend donc que si des conden­sa­teurs en paral­lèle voient leurs capa­ci­tés s’ad­di­tion­ner, ce genre de montage aura l’avan­tage de four­nir une plus grande réserve de courant, par exemple dans une alimen­ta­tion. Cela jouera ensuite sur la puis­sance que pourra déli­vrer le circuit (car, rappe­lez vous, la puis­sance est le produit de la tension et du courant).

Induc­tances en paral­lèles

Des induc­tances (ou auto-induc­tances) montées en paral­lèles voient leur valeur totale dimi­nuer, exac­te­ment de la même manière que des résis­tances. Ici, ce qui nous inté­resse c’est leur induc­tance (L), c’est-à-dire leur sensi­bi­lité au phéno­mène d’in­duc­tion. Si vous galé­rez sur cette notion, n’hé­si­tez pas à aller revoir l’ar­ticle corres­pon­dant.

Le même calcul s’ap­plique ainsi : 

1/L = 1/L1 + 1/L2 + 1/L3…

L’in­duc­tance totale sera donc toujours infé­rieure à la valeur de l’in­duc­tance la plus faible du montage.

La tension aux bornes de chaque induc­tance sera égale à la tension du géné­ra­teur.

Pour ce qui est de l’inten­sité du courant, la Loi d’Ohm s’ap­plique, sur le même modèle que les résis­tances en série. Toute­fois atten­tion ! Il y a deux cas spéci­fiques à ne pas confondre.

Comme je l’avais expliqué dans l’ar­ticle sur les bobines, une induc­tance fonc­tionne diffé­rem­ment en régime continu et alter­na­tif. Pour un courant continu, une induc­tance agit comme une simple résis­tance. Si vous voulez connaître l’in­ten­sité du courant qui traverse une de vos induc­tances, il vous suffit d’en mesu­rer la résis­tance et d’ap­pliquer la Loi d’Ohm.

En revanche, dans le cas d’un courant alter­na­tif, l’in­duc­tance oppose une autre forme de résis­tance, qui se nomme « réac­tance induc­tive » (notée XL et mesu­rée en ohms, Ω). Cette réac­tance peut se calcu­ler à partir de l’in­duc­tance L. Voici son calcul, qui n’est compliqué qu’en appa­rence : 

XL = 2 . π . f . L

Exprimé en mots : Deux fois Pi fois Fréquence fois Induc­tance

Fréquence ? Eh oui, la réac­tance n’est pas la même selon la fréquence du courant alter­na­tif. Dans l’équa­tion il s’agit d’un multi­pli­ca­teur, donc logique­ment, plus la fréquence sera haute, plus la réac­tance sera élevée (une induc­tance laisse mieux passer les basses fréquences, rappe­lez-vous).

Ainsi, en régime alter­na­tif, le calcul du courant traver­sant chaque induc­tance en paral­lèle est basé sur la loi d’Ohm mais la résis­tance ® devra être rempla­cée par la réac­tance, qui devra être calcu­lée a priori selon la fréquence.

La semaine prochaine, nous termi­ne­rons sur ce sujet, et nous passe­rons en revue les montages en série, et quelques appli­ca­tions pratiques.