Dans le dernier article nous parlions des montages en parallèle, et de leurs conséquences sur la tension, l’intensité ainsi que la valeur des composants. Aujourd’hui, nous continuons sur cette voie, en nous penchant sur les montages en série.

Nous avons déjà survolé la topologie de base d’un montage en sérieet nous nous concentrerons donc pour cet article sur les conséquences de ces montages. Il serait facile pour moi de simplement proposer une suite d’équations mais, dans un souci de pédagogie, je vais essayer d’expliciter les fonctionnements internes de chaque montage.
Nous survolerons donc tour à tour les résistances, les condensateurs et les inductances.
Pour chacun de ces composants nous verrons :
- Comment se calcule leur valeur totale lorsqu’ils sont montés ensemble.
- Comment se répartissent la tension et l’intensité dans ces séries de composants.
Commençons donc par les résistances !
Résistances en série
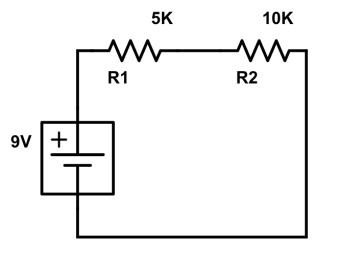
Valeur totale : pour la calculer, rien de plus simple, il suffit d’additionner :
R totale = R1 + R2 = 5 KΩ + 10 KΩ = 15 KΩ (15 000 Ω)
Intensité du courant : rappelez-vous de la Loi d’Ohm… Puisque l’on a la tension (U = 9V) et la valeur totale de la résistance (R = 15kΩ), on peut maintenant calculer l’intensité (I) du courant qui traverse ce montage.
I = U/R = 9/15000 = 0,0006 A (on notera plutôt 0,6 mA)
Dans l’article précédent, j’avais évoqué la Loi des Nœuds, qui concernait la division des courants dans des bifurcations (des « nœuds »). Ici, pas de bifurcation, pas de division : l’intensité du courant est la même partout dans le montage.
Tension : En revanche, pour ce qui est de la tension, il se passe un phénomène intéressant, et qui pourra être mis à profit dans différents circuits. Je m’explique :
Comme nous l’avions vu auparavant, la tension est une différence de potentiel et se mesure donc toujours entre deux points au sein d’un circuit. De plus, comme je l’ai déjà plusieurs fois répété, la tension se forme lorsqu’un courant rencontre une résistance, et se mesure aux bornes de cette résistance.
Avec deux résistances différentes dans notre schéma, la question se pose donc : la tension à leur bornes respectives sera-t-elle différente ? Comme d’habitude, utilisons la Loi d’Ohm : on connaît le courant qui traverse ce circuit, on connaît les résistances, il suffit de traiter leur tensions respectives comme des inconnues.
Cela donne pour la résistance R1 :
UR1 = I x R1 = 0,0006 X 5000 = 3 V
Pour R2 :
UR2 = I x R2 = 0,0006 × 10000 = 6 V
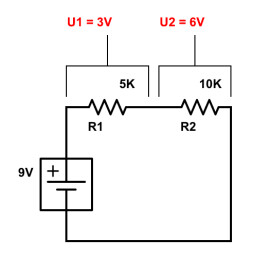
On trouve respectivement 3V aux bornes de R1 et 6V aux bornes de R2… Et 3 + 6 = 9V, la tension totale produite par le générateur ! Chaque résistance va donc diviser la tension totale selon sa valeur résistive propre. La somme des tensions aux bornes de chaque résistance sera égale à la tension totale délivrée par le générateur.
En quoi est-ce utile ? Dans ce circuit qui nous sert d’exemple, avec un générateur de 9V et un réseau de résistance en série, on a réussi à obtenir une tension de 6V qui va devenir exploitable. On appelle cela un pont diviseur.
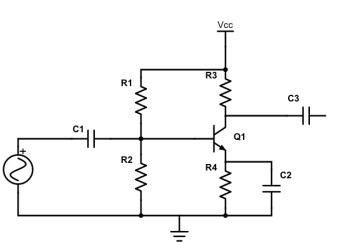
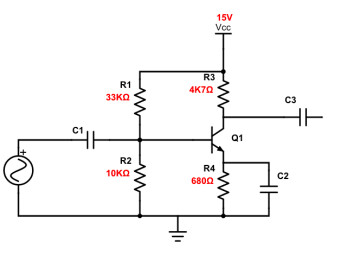
Rappelez-vous de ce schéma :
Un étage d’amplification à transistor, montage en émetteur commun
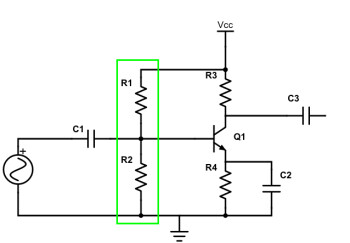
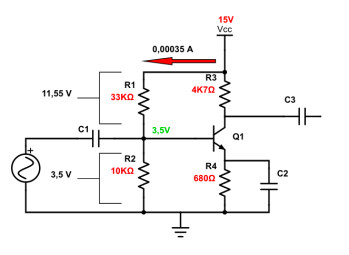
On refait le même calcul que précédemment :
Intensité du courant traversant R1 et R2 :
I = U/R = 15/43000 = 0,00035 A (attention, j’ai arrondi)
Tension respective aux bornes de R1 et R2 :
UR1 = I x R1 = 0,00035 × 33 000 = 11,55 V
UR2 = I x R2 = 0,00035 × 10 000 = 3,5 V
Ainsi, on aura 3,5V aux bornes de R2, ce qui nous permettra de polariser la base du transistor avec 3,5V (noté en vert ci-dessus). À partir d’une alimentation de 15V, on a pu dériver 3,5V pour une autre section du circuit.
Merci les résistances en série !
Condensateurs en série
On installe trois condensateurs en série (voir schéma ci-dessous). On connaît la capacité de chacun, donc ce qui nous intéresse, c’est de connaître leur capacité de charge totale. Le calcul pour obtenir cette capacité se base sur le même principe que les résistances en parallèle. Cela donne donc :
1/C = 1/C1 + 1/C2 + 1/C3…
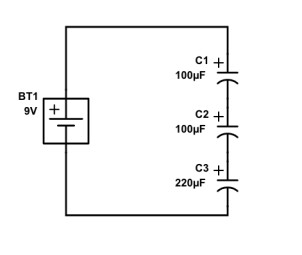
1/C totale = 1/100 + 1/ 100 + 1/220 = 40,74 µF
Comme pour les résistances en parallèle, la capacité totale est inférieure à la plus petite capacité présente dans le circuit. Monter des condensateurs en série réduit leur capacité !
Intensité du courant : Du point de vue du courant, il n’y a qu’un chemin à suivre. Sans aucune bifurcation, son intensité est la même à tous points du circuit donc I totale = IC1 = IC2 = IC3
Tension : Pour finir, la tension se répartit de façon proportionnelle aux bornes de chaque condensateur, selon sa valeur en capacité (comme pour les résistances en série ci-dessus).
Si l’on met le générateur en fonctionnement et qu’on mesure la tension aux bornes de chaque condensateur, elle sera différente selon la capacité du condensateur. Les condensateurs forment donc eux aussi un pont diviseur, comme elles résistances ci-dessus.
Inductances en série
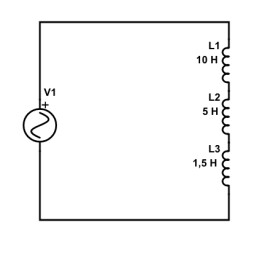
Une autre valeur qui nous intéresse : la réactance inductive. J’en ai parlé dans le dernier article mais je résume à nouveau : en courant alternatif (comme je l’ai représenté dans ce schéma ci-dessus) les inductances offrent une « résistance » différente, nommée réactance inductive, mesurée en ohms (Ω). Comme je l’avais expliqué, la valeur de la réactance est fonction de la fréquence du courant alternative qui traverse l’inductance. Ainsi, à différentes fréquences, une inductance présentera différentes réactances.
Je le redis ici, la réactance inductive d’une inductance se calcule ainsi :
XL = 2 . π . f . L
Exprimé en mots : Deux fois Pi fois Fréquence fois Inductance
Ensuite, pour un montage en série, on se contente d’additionner les réactances entre elle pour obtenir la réactance totale :
XL totale = XL1 + XL2 + XL3 …
Intensité : Encore une fois, on est dans le cas d’un montage qui possède un « chemin » unique, le courant est donc égal en tous points.
En courant continu, comme je l’avais expliqué une inductance se conduit comme une simple résistance. Il suffira de donc de mesurer (ou de connaître) la résistance de chaque inductance, de les additionner pour trouver la valeur totale en résistance. On pourra ensuite calculer l’intensité du courant traversant ce montage, comme nous l’avions fait pour les résistances.
En courant alternatif, on utilisera le même calcul en remplaçant seulement la résistance totale par la réactance inductive totale.
Tension : Là aussi, on différencie le comportement en régime continu ou alternatif, en utilisant encore la Loi d’Ohm mais en utilisant soit la résistance de chaque inductance (en continu) ou la réactance (en alternatif).
Dans les deux cas, des inductances montées en série fonctionnent un pont diviseur, avec une tension spécifique aux bornes de chaque inductance. Le calcul de chaque tension se fait sur le même modèle que pour les résistances.
Dans ces deux derniers articles, nous avons fait le tour de tous les montages parallèles ou séries pour les composants passifs. Nous avons expliqué leurs influences à la fois sur la valeur des composants et sur le courant et la tension dans un circuit. Même s’il resterait des points plus complexes que nous n’avons pas encore abordés, vous pouvez considérer ces deux articles comme une base solide pour aborder la lecture et l’analyse de schémas, en particulier pour des montages passifs (des filtres, par exemple). C’est pourquoi, au prochain article, nous nous pencherons sur des montages spécifiques, simples à réaliser, qui mettent en applications les phénomènes que nous avons étudiés jusqu’ici.