Les caractéristiques : l'impédance - L'électronique pour le musicien partie 6

Voilà donc un vaste sujet, à l’ori­gine de nombreuses ques­tions sur les forums, qui concernent géné­ra­le­ment les accords entrées-sorties, les enceintes, et la puis­sance des ampli­fi­ca­teurs. Notre site a d’ailleurs déjà consa­cré deux articles à ce sujet, l’un dans une optique sono et l’autre concer­nant les sorties d’am­plis à tubes. Qu’ap­por­ter de plus ? Notre approche : un peu plus de science, mais toujours avec l’ap­proche vulga­ri­sa­trice que nous essayons de conser­ver dans ces articles.

Impor­tant : on évite géné­ra­le­ment les angli­cismes dans nos colonnes. Toute­fois, pour plus de clarté, dans cet article, pour ne pas confondre la propriété physique que l’on nomme résis­tance, et les compo­sants du même nom, j’ap­pel­le­rai ces derniers « resis­tors ». Voilà, c’est dit, et main­te­nant on y va !

Il signe d’un Z qui veut dire…

Le sujet a déjà été abordé sur AF, il n’est plus vrai­ment un mystère, mais nous devons quand même le préci­ser avant de comment : qu’est-ce que c’est l’im­pé­dance ?

Nous l’avons déjà vu dans cette série d’ar­ticles, la résis­tance est la tendance d’un maté­riau conduc­teur à s’op­po­ser au passage du courant. L’in­verse se nomme la conduc­tance.

Nous l’avons vu, égale­ment, la résis­tance est un élément crucial dans la rela­tion entre tension et l’in­ten­sité : elle est le troi­sième élément de la Loi d’Ohm.

Tout cela est valable en régime continu (c’est à dire pour du courant continu, CC). En régime alter­na­tif (dont les signaux audio font partie), une oppo­si­tion au passage du courant existe aussi : mais cette fois-ci, on la nomme impé­dance (et on la symbo­lise Z).

Et un des éléments qui la consti­tue se nomme…

Au rayon X
 

La réac­tance. Celle-ci défi­nit spéci­fique­ment l’op­po­si­tion au courant qui se produit dans un compo­sant induc­tif (bobine) ou capa­ci­tif (conden­sa­teur). On la symbo­lise par la lettre X.

Il en existe donc deux versions :

Réac­tance induc­tive : comme on l’a vu, l’in­duc­tance s’op­pose aux varia­tions du courant. Et tout parti­cu­liè­re­ment aux varia­tions rapides (gardez-le en tête, c’est impor­tant pour notre expli­ca­tion). Puisque un courant alter­na­tif a pour carac­té­ris­tique majeure son chan­ge­ment constant (l’al­ter­nance entre posi­tif et néga­tif qui lui donne son nom), il rencon­trera une oppo­si­tion lorsqu’il traver­sera une bobine. On appelle ce phéno­mène la réac­tance induc­tive. On la symbo­lise XL.

Plus la fréquence de ce courant augmente, plus ses varia­tions sont rapides, et donc plus l’in­duc­tance s’y oppose effi­ca­ce­ment (rappe­lez-vous ce que je disais au début du para­graphe : l’in­duc­tance s’op­pose surtout aux varia­tions rapides). Donc, plus la fréquence est élevée, plus la réac­tance augmente !

En théo­rie, une bobine idéale s’op­pose moins aux fréquences graves, et plus aux aiguës : elle a un compor­te­ment théo­rique simi­laire à un filtre passe-bas.

Réac­tance capa­ci­tive : si un conden­sa­teur reçoit à ses bornes une tension conti­nue, il se charge jusqu’au maxi­mum puis bloque le courant dans le circuit (plus de dépla­ce­ments d’élec­trons à ses bornes). Mais ce phéno­mène de charge/blocage n’est pas instan­tané : il a un temps de montée. Pour une tension alter­na­tive, les varia­tions vont permettrent au conden­sa­teur de se char­ger, puis de se déchar­ger (le courant ne sera donc jamais bloqué long­temps). Mais le temps de montée a toujours un impact : plus la fréquence est basse, plus ses varia­tions sont lentes, plus le conden­sa­teur a le temps de se char­ger et de bloquer le courant. En revanche, plus la fréquence augmente (avec des varia­tions rapides), moins le conden­sa­teur a le temps de se char­ger plei­ne­ment et de bloquer le courant. On appelle ce phéno­mène la réac­tance capa­ci­tive (symbo­li­sée Xc).

En théo­rie, donc, un conden­sa­teur idéal s’op­pose moins aux fréquences aiguës, et plus aux graves : il a un compor­te­ment théo­rique simi­laire à un filtre passe-haut.

En équa­tions :

• Réac­tance induc­tive : XL = 2πfL

C’est-à-dire : 2 fois Pi fois la fréquence fois la valeur de l’in­duc­tance (mesu­rée en Henries, je vous le rappelle au passage). Je souligne : fois la fréquence ! XL est donc bien dépen­dante de la fréquence, si celle-ci augmente, XL augmente aussi. Toute­fois, si la valeur de L augmente, XL augmente égale­ment. XL est donc aussi fonc­tion de L.

• Réac­tance capa­ci­tive : XC = 1 / 2πfC

C’est-à-dire : 1 divisé par 2 fois Pi fois la fréquence fois la capa­cité (mesu­rée en Farads, je rappelle là aussi). Je souligne à nouveau : divisé par la fréquence ! Donc si la fréquence augmente, XC dimi­nue. Souli­gnons aussi que si C augmente, XC dimi­nue pareille­ment : un plus grand conden­sa­teur admet­tra donc des fréquences plus basses.

Voilà pour les conden­sa­teurs et induc­tances. Dans ces deux types de compo­sant, l’im­pé­dance Z est presque égale à X. Mais pas tout à fait… nous y revien­drons dans l’avant dernière partie !

Qu’en est-il des resis­tors ?

Pour les resis­tors, c’est beau­coup plus simple : en théo­rie leur impé­dance est égale à leur résis­tance :

 ZR = R

 ZR n’est donc pas fonc­tion de la fréquence.

Une réalité complexe

À la fin de la première partie j’ai dis que l’im­pé­dance est due, entre autres facteurs, à la réac­tance. Qu’est-ce que je voulais dire par là ?

La réac­tance étant une carac­té­ris­tique d’une induc­tance ou d’une capa­cité, on pour­rait penser que l’im­pé­dance est seule­ment réac­tive pour les bobines et les conden­sa­teurs, et résis­tive dans le cas des resis­tors. Mais ce n’est pas aussi simple.

 En effet, jusqu’ici nous avons consi­déré tous ces compo­sants comme idéaux. En réalité, chaque compo­sant passif (et cela vaut aussi pour les actifs) porte en lui ces trois proprié­tés : résis­tance, capa­cité, induc­tance.

Comment se fait-il ?

Chaque compo­sant est consti­tué de façon à ce que l’une de ces carac­té­ris­tiques soient parti­cu­liè­re­ment présente : un resis­tor résiste, un conden­sa­teur condense, une induc­tance induit. Mais leur fabri­ca­tion réelle est l’objet de compro­mis tech­niques.

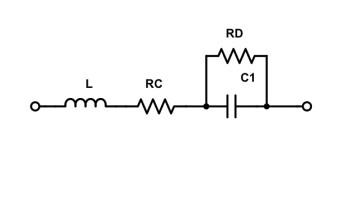
Pour expliquer cela, je commence avec le conden­sa­teur. Il est formé de deux conduc­teurs, isolés l’un de l’autre. La capa­cité de charge d’un conden­sa­teur, ainsi que sa tension maxi­male admis­sible, sont fonc­tions de la surface de ces deux conduc­teurs, et de l’iso­lant entre eux. On obtient vite deux très grandes feuilles de métals (sépa­rées par un isolant tout aussi grand). Pour gagner de la place, que fait-on ? On les enrou­le… et on obtient, géomé­trique­ment, deux bobines ! Pour cette raison, un conden­sa­teur a aussi des quali­tés induc­tives. De plus, comme ses conduc­teurs sont de grande taille (et on peut aussi leur ajou­ter les « pattes » du compo­sant) une impé­dance résis­tive, faible mais bien réelle, existe à ses bornes.

On peut donc le sché­ma­ti­ser comme ceci :

Rc repré­sente la résis­tance des connexions, et Rd la résis­tance du diélec­trique.

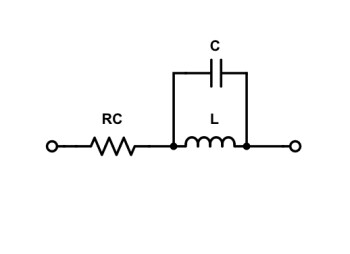
Passons ensuite à ce que nous nommons self ou auto-induc­tance. Elle possède une induc­tance L, c’est sa fonc­tion première et toute sa struc­ture est faite pour cela. Mais atten­tion, étant donné qu’elle est compo­sée d’un long conduc­teur enroulé en spires, elle a aussi une impé­dance résis­tive (faible, et qui varie selon la gros­seur et la longueur du conduc­teur, mais là aussi bien présente). Ajou­tons à cela que ses spires sont collées les unes aux autres mais sépa­rées par un isolant. Rappe­lons-le, un conden­sa­teur est formé de deux conduc­teurs sépa­rés par un isolant. Donc, par sa géomé­trie, une bobine forme plein de minus­cules conden­sa­teurs en paral­lèles.

On peut donc la sché­ma­ti­ser ainsi :

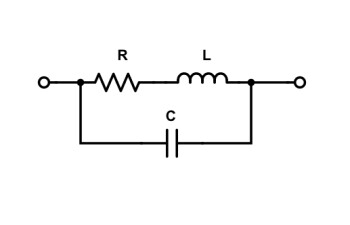
Pour finir, je vais prendre un exemple un peu exagéré mais exis­tant : un resis­tor bobiné.

La tech­no­lo­gie « bobi­née » est souvent utili­sée pour des resis­tors pouvant dissi­per de fortes puis­sances. Le resis­tor va donc présen­ter une induc­tance. Et comme on vient de l’ex­pliquer, une bobine a aussi un carac­tère capa­ci­tif ! 

Voici donc le schéma de notre resis­tor :

On comprend donc pourquoi l’im­pé­dance de chaque compo­sant est en réalité le fruit d’un accord complexe entre diffé­rents facteurs, dont certains sont dépen­dants de la fréquence et d’autres non.

Quelques calculs pour finir

Que Z soit prin­ci­pa­le­ment linéaire (dans les resis­tors) ou dépen­dante de la fréquence (bobines, conden­sa­teur) on peut géné­ra­li­ser la Loi d’Ohm au régime alter­na­tif, en écri­vant :

Z = U/I

Dans le cas des bobines et conden­sa­teurs, on doit préci­ser la fréquence f à laquelle on étudie le circuit, puisque Z est dépen­dant de f.

Pour ce qui est du montage en série d’im­pé­dances, on procède comme pour des résis­tances. Pour calcu­ler l’im­pé­dance totale :

ZT = Z1 + Z2 + Z3…

Pour des impé­dances en paral­lèle, là aussi on suit la règle qui s’ap­plique aux résis­tances :

1/ZT = 1/Z1 + 1/Z2 + 1/Z3…

Dans le prochain article, nous nous penche­rons sur les tran­sis­tors bipo­laires, et les diodes…